March 29, 2018; last revised March 24, 2025
1. In the previous post, we discussed Professor Feynman’s illustration of how two wave functions (not waves) (corresponding to two possible paths for a photon) can interfere (constructively and destructively) to produce an oscillating signal; see “Feynman’s Glass Plate Experiment.”
- It was pointed out that this experimental result is not explainable if the light is treated as an electromagnetic wave.
- More importantly, it showed that Nature instantly maps out a path for a photon as soon as it takes off.
- In this post, we will discuss his argument that “Nature takes into account ALL possible paths (an infinite number of them)”! This is our key idea behind “nonlocality,” so we will proceed step-by-step to clarify our case.
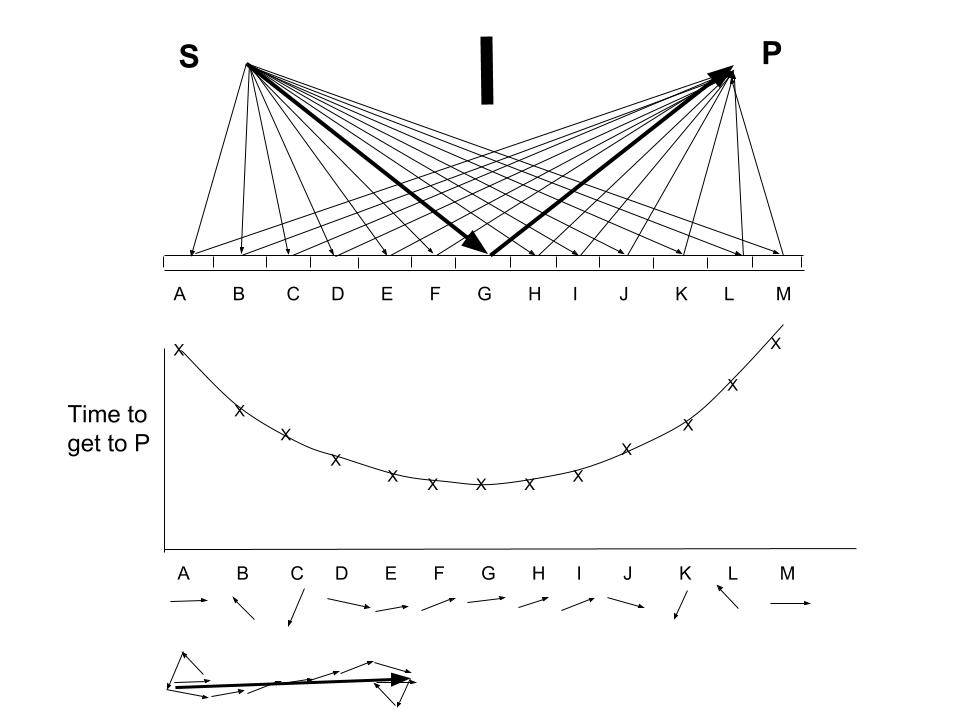
2. This discussion is also based on the following figure from Feynman’s book (p. 43); see the reference below. Light received at point P due to source S is considered; a screen between them blocks the direct path from S to P.
- Everyone is familiar with the “law of light reflection,” which states that light from A goes to Point B in a path defined by the angle incident being equal to the angle of reflection.
- Of course, the time it takes for a photon to get from S to D is minimized near the center of the mirror.
- However, Feynman showed that the concept of “a photon exploring all paths” provides a better picture with more explanatory power. He showed that most possible paths are canceled out, and only those that lie close to the expected path stated by the Law of Reflection contribute to the final detection probability.
3. To illustrate the concept of a photon “exploring all possible paths,” the mirror is divided into sections A through M, and reflection from each section of the mirror is indicated (see the above figure).
- Due to different travel distances, the time taken for each path varies (as shown in the middle figure), and correspondingly, the phase varies (as shown below using arrows). The final amplitude is given by adding those arrows, as indicated at the bottom of the figure.
4. Just like in adding the contributions from two “waves,” adding the contributions from “wave functions” requires one to take into account the difference in phase angle. Feynman has described this in simple terms, i.e., how to add contributions due to many wave functions using vector addition (see pp. 24-35).
- It is evident that the significant contribution to the final arrow’s length is made by arrows E through I (from the central part of the mirror), whose directions are nearly the same because the timing of their paths is almost the same. This also happens to be where the total time is the least indicated by the heavy arrow, which is the expected path from the law of reflection.
- The law of reflection, which we learn in high school, is a simple rule that works. However, reflections from each point in the mirror contribute to the signal at P. Most of those contributions cancel out (as shown by the bottom part of the above figure).
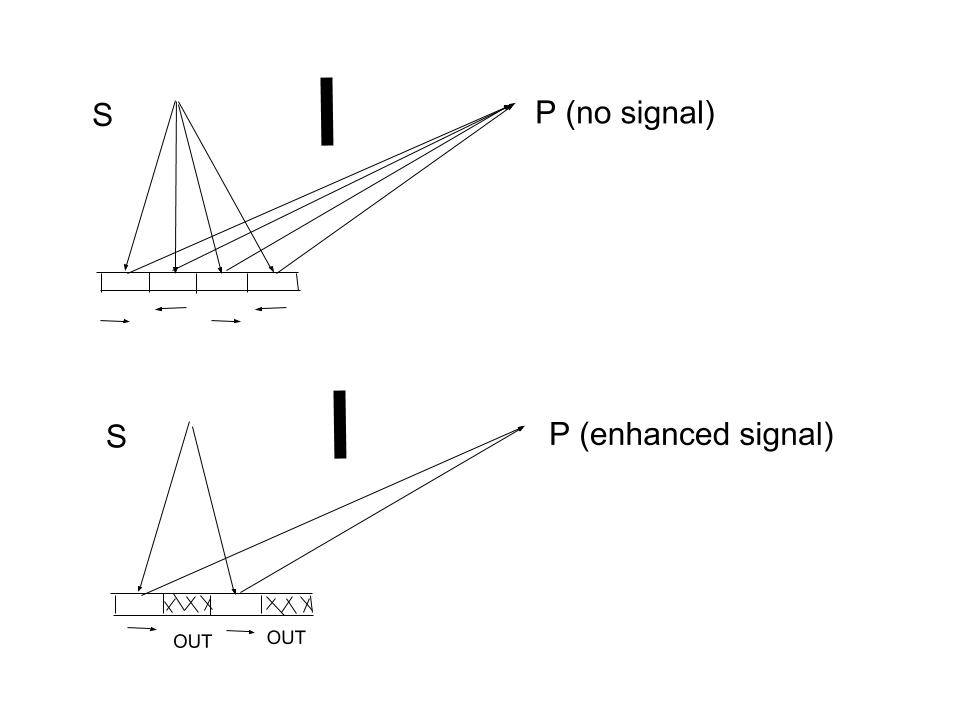
5. To prove that even the edge of the mirror contributes to the signal at P, we chop off most of the mirror, leaving only sections A, B, and C on the left. From the above figure, if we add the three arrows due to those three sections, they nearly cancel out. This is why we do not see significant contributions from parts away from the center.
- If we now divide that section (of A, B, and C in the above figure) into four equal sections, they will, of course, again cancel out, as shown in the top section of the figure below.
- But if we carefully scrape two alternating sections of those four sections (as shown in the bottom figure), the signals due to the two reflecting sections add up to give an intense signal; see the bottom part of the above figure.
6. This conclusively proves that, during normal reflection, parts of the mirror away from the center also contribute to the signal. It is just that most of that signal is canceled out. Thus, for all practical purposes, it is sufficient to take the reflection from the center part of the mirror (i.e., to use the law of reflection in geometrical optics).
- However, if only the arrows in a particular direction are kept while the others in the opposite direction are removed (by etching the mirror in those places), then a substantial amount of light reflects from a piece of mirror located away from the center, as shown in #5 above.
- That modified section of the mirror is, of course, now a diffraction grating.
7. Feynman discusses several examples in his book, but let us examine just one more example to illustrate that this method is consistent with the Principle of Causation.
- Here, we consider the case of refraction, which led to causal issues with the “photon as a particle” idea of Newton and Fermat.
- Those interested can read in detail the historical evolution of ideas from Newton through Fermat to Feynman in the book by Ivar Ekeland (see References below).
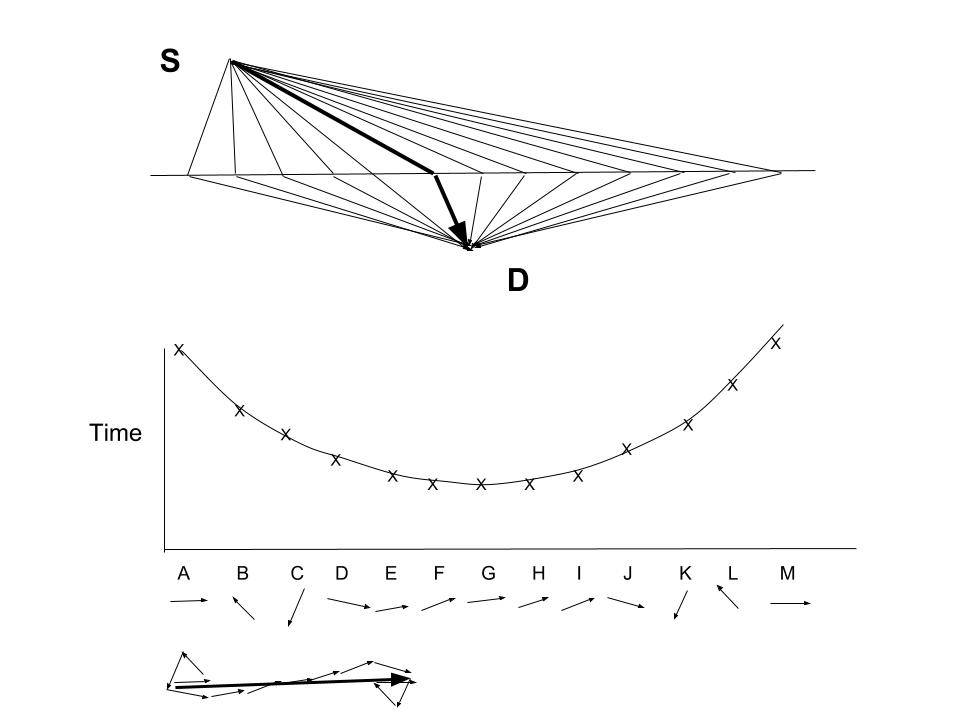
8. Figure below shows the refraction of light from a source (S) in the air to a detector (D) placed in water. As in the case of the mirror, we consider all possible paths from S to D and map out the time taken for a photon to reach point D via “different sections” of the water surface.
- The observation of light taking the “time of least time” to reach a detector in the water by changing its path (called “refraction”) was explained by Fermat back in 1657 by taking into account that light travels slower in water than in air. See “‘Exploring All Possible Paths’ Leads to Fermat’s Principle of Least Time.”
- However, until Feynman developed his method of “a particle exploring all possible paths”, this phenomenon could not be explained within the “particle picture”.
- Once again, most paths away from the optimum path are CANCELLED OUT. The significant contributions come from those paths close to the expected arrow indicated by the heavy arrow, and Fermat’s Principle of Least Time is recovered with this “particle representation.”
9. What bothered everyone (including Feynman) about Fermat’s idea is that it seemed to require agency. How could light choose a path? How could it possibly know which path was the fastest?
Here’s how Feynman puts it (Feynman Lectures, Vol. 1, Chapter 26):
“The principle of least time is a completely different philosophical principle about the way nature works. Instead of saying it is a causal thing, that when we do one thing, something else happens, and so on, it says this: we set up the situation, and light decides which is the shortest time, or the extreme one, and chooses that path. But what does it do, how does it find out? Does it smell the nearby paths, and check them against each other? The answer is, yes, it does, in a way.“
- Feynman’s method works because Nature is nonlocal. See “Will Quantum Mechanics Be Able to Explain Consciousness?” and “The Observer Effect in Quantum Mechanics.”
- A link to Feynman’s Lectures is given in the References.
An Electron Will Also Explore All Possible Paths
10. As Feynman pointed out, everything we have discussed so far can be applied to the propagation and detection of electrons: Electrons also “explore all possible paths,” and the experimental configuration determines these paths.
- If the experimental configuration changes, those paths reconfigure instantaneously. Of course, quantum electrodynamics (QED) incorporates the possible trajectories of both electrons and photons.
- Surprisingly, physicists used Feynman’s version of QED for 70 years without realizing that the same idea could be applied to quantum phenomena like the “double-slit experiment.”
Other Relevant Experiments
11. There are a couple of “real life examples” discussed in “Exploring All Possible Paths” Leads to Fermat’s Principle of Least Time.”
- Those experiments indicate that the principles we discussed are not limited to particles in the “quantum regime.”
Conclusion
12. The key philosophical problem that existed for Newton, Fermat, and Feynman with their “particle representation of light” was to explain how a photon would know in advance how to determine the path of least time.
- But that problem disappears when we realize that a photon (or any particle) takes into account “all possible paths” dictated by the nonlocality of Nature.
- First, I wanted to provide the experimental evidence from Professor Feynman’s work. I discuss nonlocality in detail in “Will Quantum Mechanics Be Able to Explain Consciousness?” and “The Observer Effect in Quantum Mechanics.”
Any questions on these QM posts can be discussed at the discussion forum: “Quantum Mechanics – A New Interpretation“.
References
I. Ekeland, “The Best of All Possible Worlds: Mathematics and Destiny”, (University of Chicago Press, 2006).
R. P. Feynman, “QED: The Strange Theory of Light and Matter” (Princeton University Press, 1985).
The Feynman Lectures on Physics, Volume I
The Feynman Lectures on Physics, Volume II
The Feynman Lectures on Physics, Volume III
