Feynman’s Glass Plate Experiment From "QED: The Strange Theory Of Light And Matter"

March 16, 2018; revised March 25, 2018

1. Feynman’s glass plate experiment that he discussed in pages 17 – 35 in his book (see the References below) is discussed in order to lay the foundation for our new interpretation of quantum mechanics (QM).

This is a key post that lays the foundation for the “nonlocality” argument. Even before I explain in detail what “nonlocality” is, I want to illustrate the simple fundamental idea behind it.

This idea is: Even before a particle takes off, Nature evaluates all possible paths that particle could take, and come up “with a plan” for its motion. This happens AUTOMATICALLY and some “unconventional paths” could result only in the case of microscopic particles like electrons and photons.
This is why quantum mechanics appear to reveal “strange phenomena”. But when particles increase in size, this “unusual behavior” goes away naturally.
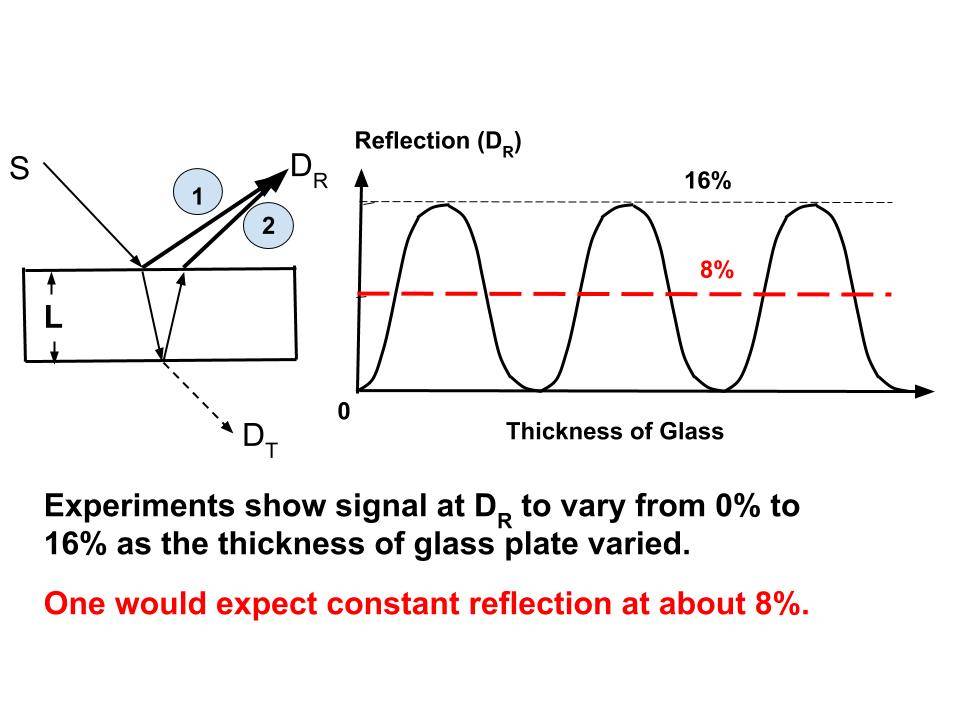
This simple idea that the physicist Richard Feynman came up is best illustrated with a simple experiment that is discussed in his book (see the References below). That experimental setup and the key result is shown in the figure below.

2. There are two “special features” in this experiment (it could be easier to print the post and read):

The two surfaces of the glass slab are well-polished and are parallel to each other with high accuracy.
The light is monochromatic, which means it has a well-defined wavelength.

3. Light from the source (S) is incident on a glass plate. Part of the light is reflected as indicated by the arrow labelled #1, and the rest is transmitted through the glass and incident on the second surface where a part of it is reflected and goes back up as indicated by the arrow #2. Rest of light emerges from the other side of the glass plate indicated by the dotted arrow. Two more things to be noted:

What is plotted on the right side of the figure is the light signal in the reflected beams #1 and #2.
Variable on the X-axis of that figure is the thickness of the glass plate (L).

4. The first thing one would expect is to have a fraction of light (about 8%) to be reflected via path #1. In fact, that is what one WILL observe with normal light (with all wavelengths in the visible region).

However, as we can see in the experimental data to the right in the figure, that reflected signal varies from 0% to 16% as the thickness of the glass plate in increased for light with a well-defined wavelength (like from a laser).
It is interesting to see that the reflected signal is zero (very low) at some thicknesses of the glass plate. This is a KEY feature that cannot be explained without our interpretation of QM. If anyone can, please post at the discussion forum. Feynman explicitly said that he could not, on p. 10 of his book.

5. Normally, one would expect the light reflected from the front surface (#1) to be at a constant level since photons are particles, i.e., a photon hitting the first surface would have no idea whether another interface existed below or not. Again, this is the key to the puzzle.

For an analogy, we can consider the following case. Imagine a wire fence with holes a bit larger than a ball that we throw at it. Some balls (those that align with the holes) will go through those holes and others will bounce back. Would it make any difference to the number of balls that bounce back if we install another fence a little bit beyond the first fence? Would it matter how far apart the fences are? Of course not.
That is a reasonable analogy that shows how amazing the above observations — seen with the glass plate and the particles of light (photons) — are.
But such effects are seen only in the microscopic realm, as we will discuss later.

6. The following is how Feynman devised a “rule” that turned out to be able to account for those observations in the figure above.

For a photon to get to the detector D_R, there are two paths available via the glass plate (#1 and #2), as shown in the figure. Feynman’s key assumption was that wave functions are established instantaneously via both those paths, and the vector sum of them would determine the possible path for a photon. These are not real waves, but just mathematical functions.
In quantum electrodynamics (QED), this procedure of “summing up all possible paths” is given the fancy name, “path integrals”.
When the path difference between those two paths is equal to the wavelength of the light, those two contributions are cancelled out (there is a phase shift of 180⁰ for the two paths in addition). That is why one sees zero intensity at plate thicknesses that are multiples of even number of half the wavelength.
On the other hand, when the path difference between those two paths is equal to the half of the wavelength of the light, those two contributions add together. That is why one sees large intensity at plate thicknesses that are odd multiples of half the wavelength.
Those are just technical details. Don’r worry about them if you are “non-technical”.

7. As long as one uses monochromatic light (and glass with no defects), one could in principle make the width of the plate arbitrarily large and those oscillations in the signal in the above figure persist. Thus as long as those two possible paths are available (without any defects in the glass plate), the resultant wave function will enforce “no reflection” at the front surface regardless of how thick the glass plate is.

On p. 21 of his book (Feynman, 1985), Feynman says, “..Today, with lasers (which produce a very pure, monochromatic light), we can see this cycle still going strong after more than 100,000,000 repetitions — which corresponds to glass that is more than 50 meters thick..“. This is an amazing observation!

8. Therefore, QM wave functions — which take into account the phases and amplitudes of all possible paths — are established instantaneously. This is a consequence of the nonlocality of nature that we will discuss in detail in upcoming posts.

In the case of the above figure, there are two possible paths for a given photon — indicated by the arrows #1 and #2 — leading to D_Ras shown in the figure. It is important to note that the path of a given photon leaving the source (S) is predetermined from the start.
Thus the question does not arise as to how the photon coming to the first surface “knows” that there is a second surface below it. There is no causality problem here, since the QM wave function is established at the very beginning because of the nonlocality of nature; if any changes are made to the experimental setup, the wave function will adjust instantaneously. Nonlocality means exactly that: physical proximity is not needed for this mechanism to work.

9. Now we will discuss a critical implication of Feynman’s “a particle exploring all possible paths” or “path integral” approach, that even Feynman did not realize.

What happens when we increase the thickness of the (defect-free) glass plate to a value that is greater than the distance from the glass plate to the detector D_R?
Now, a photon reflecting off of the front surface would have had time to reach the detector before another photon going through the glass plate even reaches the lower glass-air surface, and start coming back to the detector D_R via #2 path.
You need to take time and think about this. That is why it could be better to print the post and read. I don’t think the reviewers of our paper even realized this key point; see, bullet #3 of “Quantum Mechanics and Dhamma – Introduction“.

10. Therefore, in the absence of wave functions establishing instantaneously across both possible paths (and thus undergoing destructive interference), there CANNOT be a zero signal at the detector D_R, for ANY thickness of the glass plate if that thickness (L) is greater than the distance from the glass plate to the detector D_R.

This is the second aspect of the key observation that cannot be explained without our proposed interpretation of QM.
Again, please make comments at the discussion forum, if anyone can explain this observation in another way.

11. With the above observation, this experiment also confirms that photons are not waves, which we established in the post, “Photons Are Particles Not Waves“. In principle, two waves coming off of the front and back surfaces of the glass plate COULD destructively interfere to yield the zero intensities at those plate thicknesses.

However, in this particular case (thickness of the glass plate larger than the distance from the glass plate to the detector D_R), the “light wave” from the front surface would have arrived at the detector and be gone, by the time “light wave” from the back surface of the glass surface arrives at the detector.
Therefore, destructive interference at the detector cannot take place in the case of real waves propagating at the speed of light. What undergoes destructive interference are the mathematical wave functions representing a photon.
This is why it is important to distinguish between waves and wave functions; see, “What Is a Wave and What Is a Particle?“.

12. Therefore, the zero intensity observed at some plate thicknesses is not due to the destructive interference of waves. Instead it is due to the combined contributions from those two paths (two wave functions).

If the two wave functions destructively interfere, then not even a single photon will be directed via either of those paths, and all incident photons will go through the glass slab.
If the two wave functions interfere constructively, then maximum possible number of photons will be directed via those paths, and maximum possible signal (16%) will be observed at D_R; rest of the photons will go through the glass slab.

13. Therefore, it is very important to understand the difference between waves and wave functions. Light cannot be really called electromagnetic waves, even though the term is used even today. We have established that in the post, “Photons Are Particles Not Waves“. I am proceeding slowly to establish a solid foundation, so that questions like this do not arise later on.

Feynman’s method says that even before a particle starts moving, wave functions for “all possible paths” for that particle are established instantaneously. The particle will then move along a path that results from the “summation over all those paths”.
These wave functions are vectors (i.e., they have a magnitude and a direction). Therefore, vector addition must be used in “summing up all possible paths”. For those who are “non-technical” such details can be skipped; just get the idea.
This vector addition using a simple method with arrows is described by Professor Feynman in his book and also in a series of four public lectures (see the References below).

14. To summarize the above discussion in another way, let me quote from Feynman’s book (p.36):

“This strange phenomenon of partial reflection by two surfaces can be explained for intense light by a theory of waves, but the wave theory cannot explain how the detector makes equally loud clicks as the light gets dimmer. Quantum electrodynamics “resolves” this wave-particle duality by saying that light is made of particles, but the price of this great advancement of science is retreat by physics to the position of being able to calculate only the probability that a photon will hit a detector, without offering a good model of how it actually happens“.
Our proposed theory shows exactly how it happens.

15. As we will discuss in the upcoming posts, we point out that Feynman’s idea of a photon exploring all possible paths is none other than the enforcement of nonlocality; Feynman’s QED implicitly assumed nonlocality.

A wave function is instantaneously set up over all space taking into account the phases for all possible paths; there is no spatial limitation. This is why two particles across the universe could be still entangled; see, “Quantum Entanglement – We Are All Connected“.
In the next post we will show that in the above case, a photon will actually “explore ALL possible paths”, an infinite number of them! However, only those two paths actually came into play in the above discussion, because all others cancel out at ALL TIMES.

Any questions on these QM posts can be discussed at the discussion forum: “Quantum Mechanics – A New Interpretation“.

REFERENCES

1. Richard Feynman, “QED: The Strange Theory of Light and Matter”, Princeton University Press (1985).

2. The above book is based on a set of simple lectures delivered to non-physicists, and could be useful especially if one does not have access to the book:
QED: Photons — Corpuscles of Light — Richard Feynman (1/4)