March 13, 2018; revised August 29, 2022
Summary: Photons are ALWAYS particles. They travel as particles and are detected as particles. But the position of a photon during travel cannot be pinned down to a point (due to the Heisenberg uncertainty principle; see, “What Is a Wave and What Is a Particle?”). Only POSSIBLE LOCATIONS of the photon at any time (and the probability of detection at each location) are provided by the wave function that represents the photon. The difference between a wave and a wave function was discussed in the previous post.
1. I must warn you that this post could be too advanced for many people. However, this is the sort of “deepest level” that we will go to in this section, and if one can at least comprehend the basic idea, then one should be able the follow the future posts. The basic idea that I am trying to express is that light consists of particles called photons.
- What is meant by a “wave” in wave-particle duality is vague, and people interpret the term differently. Therefore, resolving what is meant by a “wave” in “wave-particle” duality is helpful. Is it a “real wave” like a water wave, or is it a mathematical function?
- As shown below, it has been confirmed that photons are particles, and the word “wave” SHOULD NOT be used to describe light. But, the motion of a photon can be REPRESENTED by a wave function; it is a mathematical representation.
2. For example, a statement that is made frequently is, “..the position of a single particle is spread out over space..”. This is a misleading statement and should never be used. A particle always occupies a localized position; what is spread out is the wave function, indicating possible positions for the particle to be at a given time. See the summary statement above.
- A particle, whether an electron or a photon, is detected at a detector as a single detection event. When light — reduced to low intensity — is detected at a detector, those photons are registered as “single clicks.”
- Therefore, we should give up the notion of light as a “wave.” Light consists of photons; each photon may be represented by a wave function, which is a mathematical concept. This lingering and false idea of a “wave” is the main obstacle to having a unified theory of QM.
3. Newton believed that light consisted of particles. Newton’s corpuscular theory of light prevailed until around 1850 when it was abandoned because it could not explain light’s interference and diffraction effects. Since then, light has been regarded as a wave for a while.
- But starting around 1900, that wave picture could not account for many new experimental observations, including the photoelectric effect, black-body radiation, and Compton scattering. Einstein proposed that light is quantized to explain the photoelectric effect (Einstein, 1905) — for which he received the Nobel Prize in physics in 1921 — and those quanta were given the name photon; they are the original “quanta” of quantum mechanics.
- Compton (Compton 1923) confirmed that a photon is a particle with momentum, for which he received the Nobel Prize in 1927.
- The photon concept has led to momentous advances in experimental and theoretical physics, such as lasers, Bose-Einstein condensation, and quantum field theory.
4. Then, in 1948, Feynman illustrated that it is not necessary to consider photons as waves at all (Feynman, 1948; Feynman, 1949; Feynman, 1985).
- While the first two references above are technical papers, the third one is a book written in very simple terms. I would recommend those who are interested to read the book. I am only going to summarize what is in the book.
- That book was based on a series of 4 lectures. These are simple lectures delivered to non-physicists and could be useful, especially if one does not have access to the book:
QED: Photons — Corpuscles of Light — Richard Feynman (1/4)
5. However, there was a persistent view up to 1986 that light could not be particles and that many effects, such as the photoelectric effect, can be explained without the concept of a photon (Lamb and Scully, 1968; Crisp and Jaynes, 1969; Mandel, 1976).
- The final confirmation of a photon as a particle had to wait until single-photon sources were developed. In 1986 Granger, Roger, and Aspect confirmed in their anticorrelation experiments that photons are indeed particles. We discuss this experiment below.
Proof That Photons Are Particles
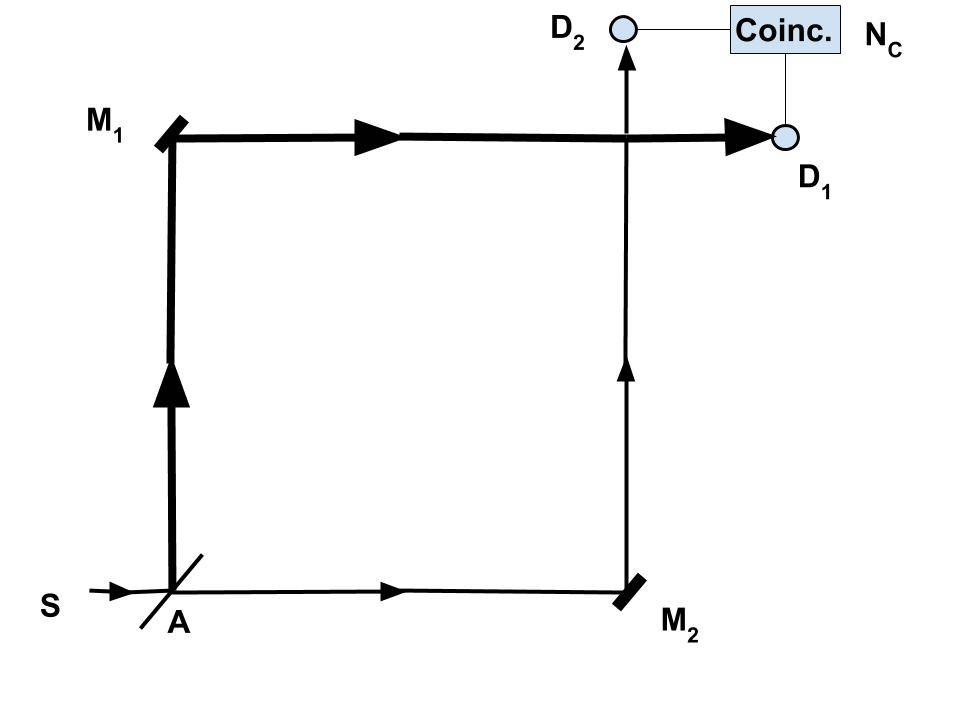
The figure below shows the experimental configuration used by Granger, Roger, and Aspect to verify that photons are indeed particles (Granger, Roger, and Aspect, 1986).
1. Single photons generated at S are sent through a beam splitter, and a signal via each leg is detected at D1 and D2. In this experiment, one photon at a time is incident on the beam splitter A.
- If a photon is a particle, it can be either reflected at A and go towards mirror M1, which will then be detected at detector D1, OR, it could go through A, reflected by mirror M2, and detected at detector D2. Then a detection would register only at D1 or D2.
- However, if the photon is a wave, it could partially propagate through each arm and be detected at both D1 and D2 simultaneously. That would count as a “coincidence count (NC).”
- If a photon sometimes acts like a wave, there should be some coincidence counts.
2. The experiments confirmed that a given photon always takes one path at a time (Granger, Roger, and Aspect, 1986).
- This experiment conclusively proved that a photon travels either via path A M1 D1 or path A M2 D2.
- If photons had the “wave nature,” there would have been at least some coincidence counts.
3. With this experimental confirmation, a photon is now categorized as an elementary particle. A photon at any wavelength is detected as a particle.
- In Feynman’s Quantum Electrodynamics (QED), a photon is successfully treated as a particle that takes into account “all possible paths” via path integrals.
- In our proposed theory, a photon is a particle, and its motion is governed by a mathematical wave function set up instantaneously across space taking into account the details of the experimental arrangement; this wave function explains interference and diffraction effects.
4. Newton’s corpuscular theory of light was abandoned around 1850 because it could not explain interference and diffraction phenomena.
- However, when Feynman introduced his new approach to quantum mechanics in 1948, he proposed that “.The probability that a particle will be found to have a path x(t) lying somewhere within a region of space-time is the square of a sum of contributions, one from each path in the region. The contribution from a single path is postulated to be an exponential whose (imaginary) phase is the classical action (in units of ℏ) for the path in question..” (Feynman, 1948, p. 367).
- Then he applied that concept to describe the propagation of photons and electrons in his formulation of quantum electrodynamics (QED); see (Feynman, 1949). The basic idea of photon propagation using “all possible paths available” has been explained by Feynman in his introductory book (Feynman, 1985) on QED.
5. Feynman explained his theory of QED with simple diagrams without equations in his book (Feynman, 1985). See “Basis of the Proposed Interpretation – Feynman’s Technique in QED.”
- However, his technique was completely ad hoc; there was no rationale behind it. As he explained (p. 10 of Feynman, 1985): “..what I am telling you is, while I am describing how Nature works, you won’t understand why Nature works that way. But you see, nobody understands that. I can’t explain why Nature behaves in this particular way”.
- With new experimental results published since then, we can now understand the rationale behind his technique. That is what we will be discussing in the first series of posts and is also in the unpublished paper: “A Self-Consistent Interpretation of Quantum Mechanics Based on Nonlocality.”
6. Of course, many phenomena involving light can be explained with light treated as an electromagnetic (EM) wave, just like the motion of large particles can be treated with Newtonian mechanics.
- But when analyzing quantum phenomena, the EM theory does not work for light, and the Newtonian mechanics does not work for microscopic particles. This is quite apparent in QED, which deals with the interactions of light with electrons.
Any questions on these QM posts can be discussed at the discussion forum: “Quantum Mechanics – A New Interpretation.”
REFERENCES (Click to download the pdf)
Compton, A. H., A Quantum Theory of the Scattering of X-Rays by Light Elements (1923)
Crisp, M.D., Radiative effects in semiclassical theory (1969)
English Translation of Einstein-Generation and conversion of light with regard to a heuristic point of view (1905)
Feynman, R.P. Space-Time Approach to Non-Relativistic Quantum Mechanics (1948)
Feynman, R.P. Space-Time Approach to Quantum Electrodynamics (1949)
Feynman, R.P., QED: The Strange Theory of Light and Matter, Princeton University Press (1985).
Grainger, P. et al Experimental Evidence for a Photon Anticorrelation Effect (1986)
Lamb, W. E. and M. O. Scully, The Photoelectric effect without photons (1968). Available online at The Photoelectric effect without photons
Mandel. L., The case for and against semiclassical radiation theory, in Progress in Optics, vol. 13, North-Holland (1976). (pdf not available).