April 1, 2018; last revised March 24, 2025
Why Does Light Bend When Entering Water?
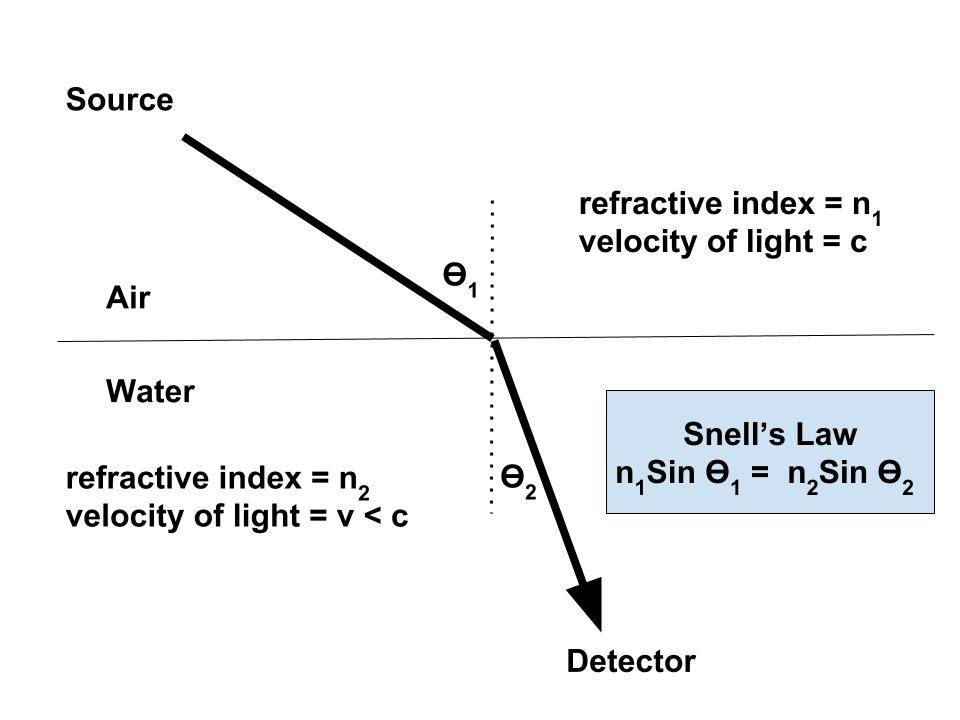
1. In 1657, the French lawyer and mathematician Pierre De Fermat (behind Fermat’s Last Theorem) worked out that when light travels from one place to another, it always takes the path of least time. The path of a ray of light going from air to water is shown below.
- There’s a formula called Snell’s law (shown in the figure) that correctly predicts the exact angle by which the light bends, depending on the materials it’s traveling through and the angle at which it hits the surface.
- Fermat explained this observation of light taking the “time of least time” to reach a detector in the water and changing its path (called “refraction”) by taking into account that light travels slower in water than in air.
- But the question of WHY it does that has not been answered. Furthermore, how would a photon know an interface is coming up ahead? As we saw in the post, “Feynman’s Method of “A Particle Exploring All Possible Paths,” the wave theory of light cannot explain it.
- As we also saw in that post, Feynman devised a technique called “a photon exploring all possible paths” but admitted that he did not know WHY it worked. In future posts, we will show that it is due to the nonlocality of Nature and the instantaneous establishment of quantum fields for “all possible paths” for the photon.
A Swimmer Does the Same as Light!
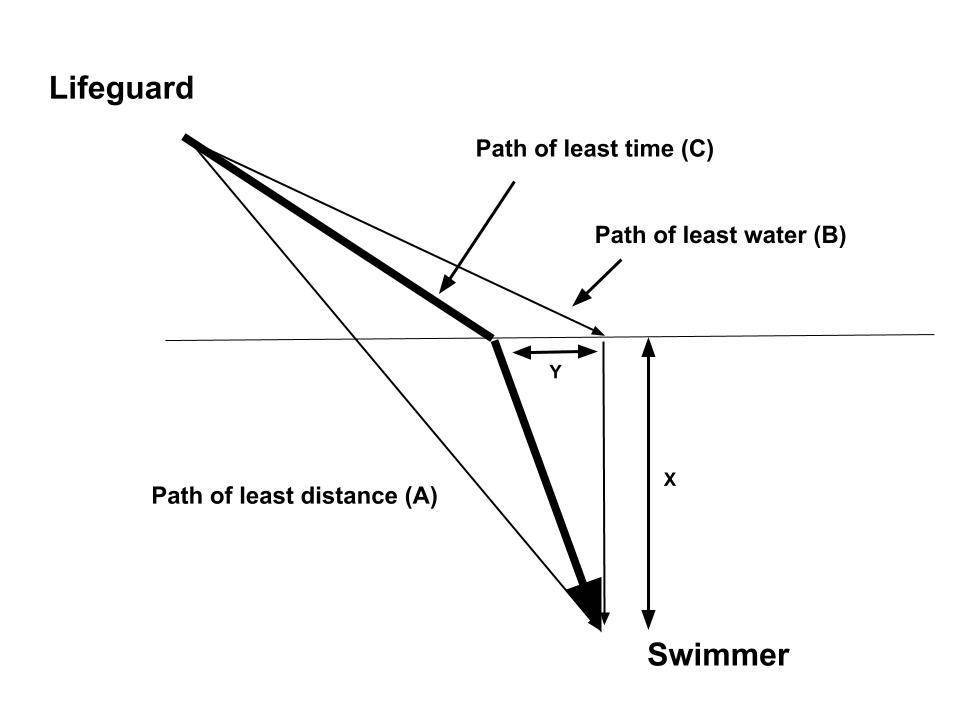
2. That is precisely the same procedure followed by a lifeguard (instinctively) in reaching a drowning swimmer in the water. The figure below illustrates the situation.
How to Find the Path of Least Time?
3. When we look at the above figure, at first glance, one may wonder whether a straight line (path A) is the fastest path. That is indeed the shortest, but it isn’t the quickest because one can run faster along the beach and cover more distance on land than on the water.
- However, if one runs on path B, making the distance in water minimum is also not the quickest. That route is too long, and it slows you down.
- The quickest path is C, which lies between A and B, where the lifeguard jumps in at a distance of x before the shortest path in the water.
- Of course, a lifeguard would not even think about all this. Instead, he/she would instinctively choose a path that turns out to be close to this optimum path C.
An Experiment on a Dog
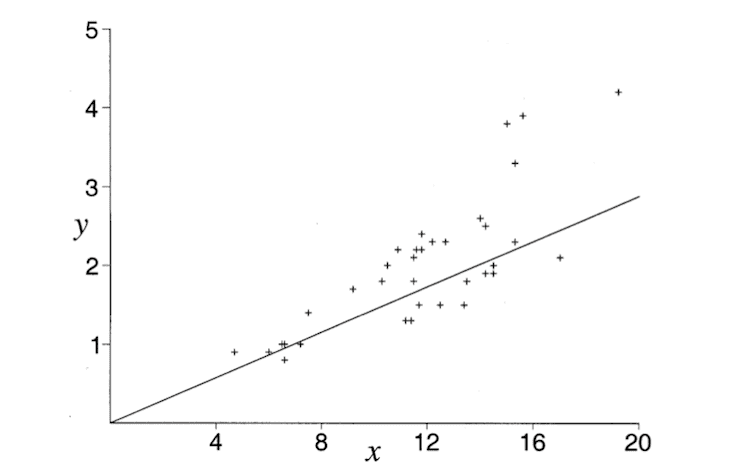
4. I have not encountered anyone experimenting on lifeguards and seeing how close they get to the “optimum path.” But I came across a paper by a math professor who studied his dog fetching a ball thrown into Lake Michigan.
- He found that his dog’s path (over many measurements) came close to the “optimum path” predicted by Snell’s law: “Do Dogs Know Calculus- Pennings-2003“.
5. After collecting 35 data points (the x and y values in the figure above, in meters), Professor Pennings plotted them. Along with these data points, he also drew the optimal trajectory predicted by Snell’s law, shown by the straight line below (figure from the above paper).
- Therefore, just like a photon “would know” how to take the “path of least time,” a dog would too!
Ants Take the Path of Least Time Too!
6. Even more interestingly, even ants seem to find the “optimum path” that takes the least time to get to their food.
- A group of researchers used a glass surface and a rough green felt surface—analogous to air and water or sand and water in the above cases—to separate a colony of ants. They placed ant food some distance into the rough green felt surface.
- They found that the ant trails were far closer to the quickest path than to the direct route. Like light and lifeguards, these ants seemed to minimize time and not distance. The following figure showing the ants’ trail is from their paper: “Fermat’s Principle of Least Time Predicts Refraction of Ant Trails at Substrate Borders.”
Conclusion
The critical philosophical problem for Newton, Fermat, and Feynman with their “particle representation of light” was to explain “how a photon would know” in advance how to determine the path of least time; see the book by Ivar Ekeland in the References.
- But that problem goes away when we realize that a photon (or any particle) takes into account “all possible paths” instantaneously due to Nature’s nonlocality. That is the basis of our new interpretation of quantum mechanics. We will discuss this in detail in upcoming posts.
- Interestingly, the observations that humans, dogs, and ants all take the “path of least time” instinctively illustrate that this is how Nature works. Even living beings are guided by this “nonlocality of Nature.” This example demonstrates that there is so much that we DO NOT KNOW about how Nature works.
- That is closely related to how Nature AUTOMATICALLY executes kamma vipāka. That will become more clear as we proceed. Also see “Quantum Entanglement – We Are All Connected.”
We can discuss any questions on these QM posts at the discussion forum: “Quantum Mechanics – A New Interpretation.”
References
I. Ekeland, “The Best of All Possible Worlds: Mathematics and Destiny” (University of Chicago Press, 2006).
R. P. Feynman, “QED: The Strange Theory of Light and Matter” (Princeton University Press, 1985).
J. Oettler et al., “Fermat’s Principle of Least Time Predicts Refraction of Ant Trails at Substrate Borders,” PLOS ONE, vol. 8, issue 3, e59739 (2013).
T. J. Pennings, “Do Dogs Know Calculus?“, The College Mathematics Journal, vol. 34, No. 3, pp. 178-182 (2003); link to pdf in #4 above.